문제
직선으로 되어있는 도로의 한 편에 가로수가 임의의 간격으로 심어져있다. KOI 시에서는 가로수들이 모두 같은 간격이 되도록 가로수를 추가로 심는 사업을 추진하고 있다. KOI 시에서는 예산문제로 가능한 한 가장 적은 수의 나무를 심고 싶다.
편의상 가로수의 위치는 기준점으로 부터 떨어져 있는 거리로 표현되며, 가로수의 위치는 모두 양의 정수이다.
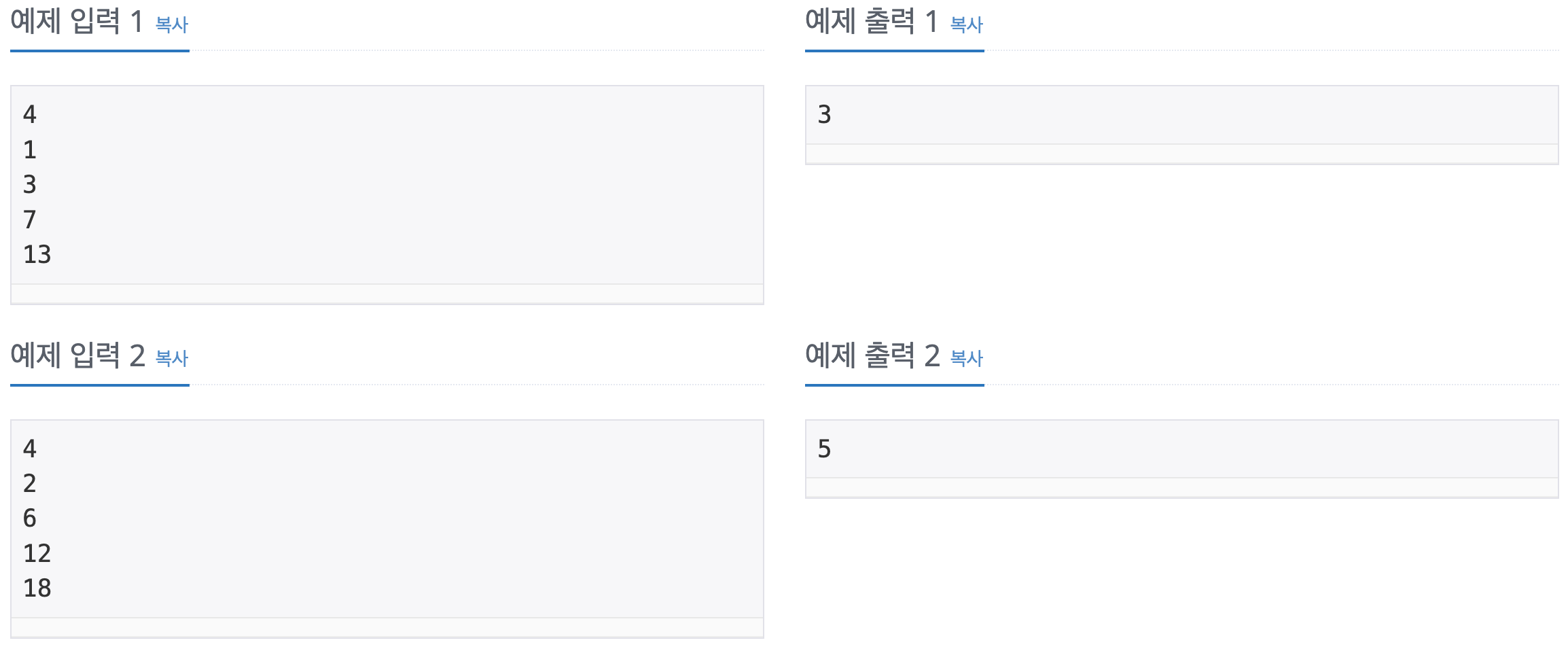
예를 들어, 가로수가 (1, 3, 7, 13)의 위치에 있다면 (5, 9, 11)의 위치에 가로수를 더 심으면 모든 가로수들의 간격이 같게 된다. 또한, 가로수가 (2, 6, 12, 18)에 있다면 (4, 8, 10, 14, 16)에 가로수를 더 심어야 한다.
심어져 있는 가로수의 위치가 주어질 때, 모든 가로수가 같은 간격이 되도록 새로 심어야 하는 가로수의 최소수를 구하는 프로그램을 작성하라. 단, 추가되는 나무는 기존의 나무들 사이에만 심을 수 있다.
입력
첫째 줄에는 이미 심어져 있는 가로수의 수를 나타내는 하나의 정수 N이 주어진다(3 ≤ N ≤ 100,000). 둘째 줄부터 N개의 줄에는 각 줄마다 심어져 있는 가로수의 위치가 양의 정수로 주어지며, 가로수의 위치를 나타내는 정수는 1,000,000,000 이하이다. 가로수의 위치를 나타내는 정수는 모두 다르고, N개의 가로수는 기준점으로부터 떨어진 거리가 가까운 순서대로 주어진다.
출력
모든 가로수가 같은 간격이 되도록 새로 심어야 하는 가로수의 최소수를 첫 번째 줄에 출력한다.
풀이
가로수 간격 사이의 최대공약수를 구해서 현재 심어진 가로수를 제외한 나머지 개수를 구하는 문제이다.
수행 순서는 다음과 같다.
1. 현재 가로수 개수를 입력받는다.
2. 작은수부터 정렬한 후 첫 번째와 두 번째 가로수 사이의 간격을 최대공약수로 정한다.
3. 두 번째 가로수부터 반복문을 실시하여 각 간격의 최대공약수를 구한다.
4. 시작과 끝 가로수의 길이를 최대공약수로 나누고 1을 더한 후 현재 심어진 가로수의 개수를 빼준 값을 출력한다.
(최대공약수로 나눈 값은 시작과 끝 중 하나만 고려한 값이므로 1을 더한다.)
설명보다는 코드를 보는것이 이해하는 데 더 쉬울 것 같다.
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.Arrays;
public class Main {
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
int N = Integer.parseInt(br.readLine());
int[] arr = new int[N];
for(int i = 0; i < N; i++) {
arr[i] = Integer.parseInt(br.readLine());
}
Arrays.sort(arr);
int gcd = arr[1] - arr[0];
for(int i = 1; i < N - 1; i++) {
int distance = arr[i+1] - arr[i];
gcd = getGCD(distance, gcd);
}
System.out.println(((arr[arr.length-1] - arr[0]) / gcd) + 1 - N);
}
public static int getGCD(int num1, int num2) {
if(num1 % num2 == 0) {
return num2;
}
return getGCD(num2, num1%num2);
}
}
* 더 좋은 풀이방법이나 문의사항은 댓글로 달아주세요.
'백준' 카테고리의 다른 글
| [백준] 1929번 : 소수 구하기 - JAVA (0) | 2023.09.12 |
|---|---|
| [백준] 4134번 : 다음 소수 - JAVA (0) | 2023.09.12 |
| [백준] 1735번 : 분수 합 (0) | 2023.09.07 |
| [백준] 13241 : 최소공배수 (0) | 2023.09.07 |
| [백준] 1934번 : 최소공배수 (0) | 2023.09.07 |